2.2. Siły o liniach działania równoległych do siebie
2.2.1. Wypadkowa dwóch sił równoległych
Gdy na ciało sztywne działają dwie siły o nierównoległych i leżących w jednej płaszczyźnie liniach działania, siły te możemy przesunąć do punktu przecięcia się tych linii i zastąpić wypadkową w myśl prawa równoległoboku. Sposób ten zawodzi, gdy linie działania sił są do siebie równoległe.
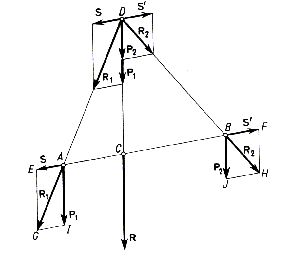
Rys. 2.11
Rysunek 2.11 przedstawia takie dwie równoległe siły P1 i P2 przyłożone do punktów A i B pewnego ciała sztywnego. Do punktów tych przyłożymy dwie równe co do wartości liczbowych i przeciwnie skierowane siły S i S' działające wzdłuż prostej AB. Mamy więc
Takie równoważące się siły można zawsze przyłożyć do ciała sztywnego. Siły P1 i S przyłożone do punktu A, oraz siły P2 i S' przyłożone do punktu B możemy zastąpić wypadkowymi
Linie działania sił R1 i R2 nie są już do siebie równoległe i przecinają się w punkcie oznaczonym na rys. 2.13 literą D. Po przesunięciu sił R1 i R2 wzdłuż tych linii do punktu D zastępujemy je wypadkową
Na podstawie (a) i (b) mamy:
Tak więc dane siły P1 i P2 przyłożone do punktów A i B zastąpiliśmy jedną siłą wypadkową R równoległą do tych sił. Wartość liczbowa tej wypadkowej równa jest w danym przypadku sumie wartości liczbowych sił P1 i P2, tj.
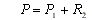 (2.14)
(2.14)
Dwie równolegle i zgodnie skierowane siły P1 i P2 przyłożone do punktów A i B ciała sztywnego zastąpić możemy równoległą i zgodnie z nimi skierowaną silą wypadkową R o wartości liczbowej równej sumie wartości liczbowych danych sil. Linia działania tej wypadkowej dzieli wewnętrznie odcinek AB odwrotnie proporcjonalnie do wartości liczbowych sil P1 i P2.
Poprzednie rozważania dotyczyły dwu sił równoległych zgodnie skierowanych. Rozpatrzmy teraz przypadek, gdy dane dwie siły równoległe mają przeciwne kierunki, tak jak na rys. 2.12. Załóżmy, że siła P1 przyłożona w punkcie A ma większą wartość liczbową, czyli P1>P2.
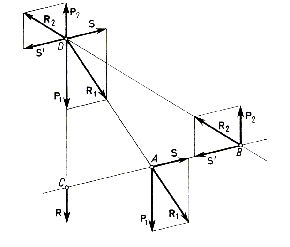
Rys. 2.12
W przypadku tym postępujemy tak jak poprzednio, tzn. do punktów A i B (rys. 2.12) przykładamy dwie równe co do wartości i przeciwnie skierowane wzdłuż tej samej prostej siły S i S'. Zastępujemy siły P1 i S wypadkową R1 oraz siły P2 i S' wypadkową R1. Przesuwamy następnie siły R1 i R2 wzdłuż ich linii działania do punktu przecięcia się tych linii i zastępujemy wypadkową:
Wartość liczbowa wypadkowej równa jest
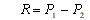 (2.15)
(2.15)
Wypadkowa R skierowana jest zgodnie z siłą o większej wartości, tj. w danym przypadku zgodnie z siłą P1.
Dwie równolegle i przeciwnie skierowane siły P1 i P2 przyłożone do punktów A i B ciała sztywnego możemy zastąpić równoległą do nich wypadkową R, skierowaną zgodnie z silą o większej wartości liczbowej. Linia działania tej wypadkowej dzieli zewnętrznie odcinek AB w stosunku odwrotnie proporcjonalnym do wartości sil przyłożonych w punktach A i B i leży po stronie większej siły. Wartość liczbowa wypadkowej R równa jest różnicy wartości liczbowych danych sil.