2.1. Siły zbieżne o liniach działania leżących w jednej płaszczyźnie

2.1.1. Znajdywanie wypadkowej sił zbieżnych

Załóżmy, ze do pewnego ciała sztywnego przyłożone są siły, których linie działania leżą w jednej płaszczyźnie i przecinają się wszystkie w jednym punkcie. Taki układ sił nazywa się płaskim układem sil zbieżnych.
Ponieważ siłę działającą na ciało sztywne można przesuwać dowolnie wzdłuż jej linii działania, siły zbieżne można traktować jako przyłożone do jednego punktu. Rysunek 2.1. przedstawia taki właśnie układ sił P₁, P₂, P₃, P₄, przyłożonych do punktu O pewnego ciała.

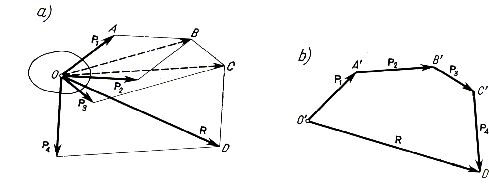
Rys. 2.1

Ponieważ dwie siły przyłożone do jednego punktu można zastąpić wypadkową według prawa równoległoboku, postąpimy tak z siłami P₁ i P₂. Otrzymujemy wówczas wypadkową, pokazaną na rysunku jako wektor OB, którą następnie możemy w podobny sposób złożyć z siłą P₃. 0trzymaną w ten sposób siłę jako wektor OC składamy dalej z siłą P₄ i otrzymujemy wreszcie jedną siłę R, którą nazywamy wypadkową danego układu sił. Powyższy sposób można zastosować dla dowolnej liczby sił.
Siłę wypadkową R możemy wyznaczyć również w inny, prostszy jeszcze sposób. Z rysunku 2.1a wynika, że wektor przedstawiający tę siłę jest bokiem zamykającym wielobok OABCD, którego pozostałe boki są równe wektorom przedstawiającym siły P₁, P₂, P₃ i P₄. Wielobok taki nazywa się wielobokiem sił. Zgodnie z definicją sumy wektorów wypadkowa R jest sumą geometryczną wszystkich sił układu.
Sumowanie geometryczne sił można wykonać osobno, tak jak pokazano na rys. 2.1b; trzeba jednak pamiętać, że wypadkową R należy przyłożyć do punktu O. Na podstawie powyższego możemy stwierdzić: dowolny płaski układ n sił P₁, P₂, ..., P_n przyłożonych do punktu O możemy zastąpić silą wypadkową R równą sumie geometrycznej tych sił i przyłożoną również do punktu O. Używając przyjętego sposobu oznaczania sumy geometrycznej mamy

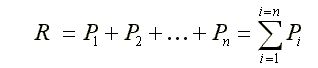(2.1)

2.1.2. Równowaga płaskiego układu sił zbieżnych

Na podstawie metody znajdowania wypadkowej płaskiego układu sił zbieżnych można wyprowadzić warunek, który spełniać muszą siły tego układu, aby znajdowały się one w równowadze. Równowaga możliwa jest oczywiście tylko wtedy, gdy wypadkowa tych sił jest równa zeru, a więc wtedy, gdy wielobok zbudowany z tych sił jest wielobokiem zamkniętym. Oznacza to, że po nakreśleniu tego wieloboku, koniec ostatniego wektora pokrywa się z początkiem pierwszego.
Na rysunku 2.2a przedstawiono układ czterech sił przyłożonych do punktu O pewnego ciała. Siły te są w równowadze, gdyż wektory ich tworzą zamknięty czworobok ABCD nakreślony na rys. 2.2b.

Rys. 2.2

Zgodnie z powyższymi rozważaniami możemy sformułować następujący warunek równowagi płaskiego układu sił zbieżnych. Aby siły zbieżne P₁, P₂, ..., P_n działające w jednej płaszczyźnie znajdowały się w równowadze, wielobok z nich zbudowany, czyli wielobok sil, musi być wielobokiem zamkniętym. Powyższemu warunkowi odpowiada następujące równanie wektorowe:

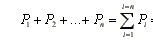(2.2)

Przy rozwiązywaniu zagadnień równowagi dotyczących układu n sił zbieżnych o określonych liniach działania musimy mieć z góry dane wartości liczbowe (n-2) sił, wartości liczbowe zaś dwóch pozostałych możemy wyznaczyć z powyższego warunku równowagi. Rysunek 2.3a przedstawia właśnie taki układ w przypadku, gdy n=5, przy czym siły P₁, P₂, P₃ są określone co do wartości i co do kierunku, siły V i W zaś mają znane tylko linie działania. Należy wyznaczyć te dwie ostatnie siły, przy założeniu, że układ jest w równowadze. W tym celu rysujemy w pewnej skali wielobok sił, zaczynając od znanych sił P₁, P₂, P₃ (rys. 2.3b).

Rys. 2.3

Następnie z początku pierwszego wektora i końca trzeciego, tj. punktów oznaczonych na rysunku przez A i D, prowadzimy proste odpowiednio równoległe do linii działania sił V i W. Proste te przecinają się w punkcie E. Wektory i przedstawiają szukane siły W i V, gdyż tworzą łącznie z siłami P₁, P₂, P₃ zamknięty wielobok sił ABCDE.

2.1.3. Równowaga trzech sił nierównoległych

Niech dane będą trzy siły P₁, P₂ i P₃ przyłożone do punktów A, B, C pewnego ciała sztywnego, o których założymy, że są w równowadze. Załóżmy jeszcze, że linie działania tych sił leżą w jednej płaszczyźnie i nie są do siebie równoległe (rys. 2.4).

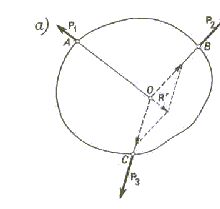
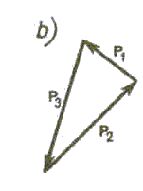
Rys. 2.4

Linie działania sił P₂ i P₃ przecinają się w punkcie oznaczonym na rysunku literą O. Siły te możemy przesunąć wzdłuż tych linii do punktu O i zastąpić następnie wypadkową

2.1.4. Analityczna metoda wyznaczania wypadkowej płaskiego układu sił zbieżnych

Rozważmy siłę P przyłożoną do punktu O pewnego ciała materialnego. Z punktu tego poprowadźmy dwie wzajemnie prostopadłe osie współrzędnych Ox i Oy leżące w jednej płaszczyźnie z linią działania siły (rys. 2.5). Proste opuszczone z końca A wektora P prostopadłe do wspomnianych osi odcinają na nich wektory OA' i OA'' , które nazywamy rzutami wektora P, czyli w danym przypadku siły, na osie układu współrzędnych. Miary względne tych wektorów oznaczmy odpowiednio przez P_x i P_y. Wielkości te nazywamy składowymi siły P w prostokątnym układzie współrzędnych Oxy.

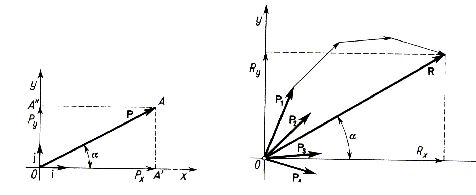
Rys. 2.5                                   Rys.2.6

Z rysunku 2.5 znajdujemy

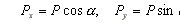(2.3)

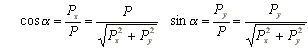(2.4)

Z rysunku 2.5 wynika, że siłę P można traktować jako wypadkową dwu sił skierowanych wzdłuż osi układu współrzędnych i przedstawionych za pomocą wektorów OA' i OA'' . Jeżeli na Ox i Oy umieścimy jednostkowe wektory i oraz j, zwane wersorami, z których każdy jest zgodnie skierowany z odpowiednią osią, to

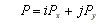(2.5)

Załóżmy teraz, że do pewnego punktu O przyłożonych jest n sił P₁, P₂, ..., P_n, których linie działania leżą w jednej płaszczyźnie. W płaszczyźnie tej obierzemy prostokątny układ współrzędnych Oxy, tak jak to przedstawia rys. 2.6 dla przypadku, gdy n=4. Rozważane siły zbieżne zastąpić możemy siłą wypadkową R równą ich sumie geometrycznej, tj.

Wyznaczymy składowe R_x i R_y wypadkowej. Oprzemy się na twierdzeniu, według którego rzut sumy geometrycznej wektorów na dowolną oś równy jest sumie rzutów tych wektorów na tę samą oś. Stosując to twierdzenie do rzutów wypadkowej R na osie Ox i Oy otrzymujemy

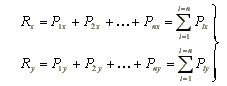(2.6)

W równaniach tych P_ix i P_iy oznaczają odpowiednie składowe siły P_i.
Po obliczeniu z równań (2.6) składowych wypadkowej R możemy wyznaczyć jej wartość liczbową oraz kąt a, który tworzy ona z osią Ox:

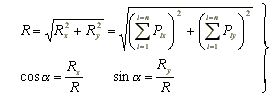(2.7)

2.1.5. Równania równowagi płaskiego układu sił zbieżnych

W podrozdziale 2.1.2 tego rozdziału znaleziono warunek, który muszą spełniać siły tworzące płaski układ sił zbieżnych, aby znajdowały się one w równowadze. Ponieważ wypadkowa R tych sił musi wówczas być równa zeru, jej rzuty na osie Ox i Oy prostokątnego układu współrzędnych, obranego dowolnie w płaszczyźnie, w której działają te siły, muszą znikać. Z zależności (2.6) wynika bezpośrednio, że w przypadku równowagi muszą być spełnione następujące dwa równania:

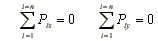(2.8)

Równania te nazywamy równaniami równowagi dla sił zbieżnych działających w jednej płaszczyźnie.
Tak więc, aby siły zbieżne leżące w jednej płaszczyźnie były w równowadze, sumy rzutów tych sil na osie układu współrzędnych muszą być równe zeru.
Przy wyprowadzaniu równań (2.8) posługiwaliśmy się prostokątnym układem współrzędnych Oxy. Jeśli jednak wypadkowa R jest równa zeru, jej rzut na jakąkolwiek oś musi być także równy zeru, a stąd wynika, że przy układaniu równań równowagi nie musimy trzymać się koniecznie prostokątnego układu współrzędnych. Wystarczy obrać po prostu dwie jakiekolwiek nierównoległe do siebie osie, leżące w płaszczyźnie, w której działają siły, i przyrównać do zera sumy rzutów wszystkich sił na te osie.

2.1.6. Moment siły względem punktu

Na rysunku 2.7 przedstawiona jest siła P przyłożona do pewnego ciała materialnego. Ramieniem siły P względem dowolnie obranego punktu O nazwiemy odległość h linii działania l tej siły od punktu O. Z określenia tego wynika, że ramię siły względem punktu jest równe zeru wtedy, gdy linia działania siły przechodzi przez dany punkt.

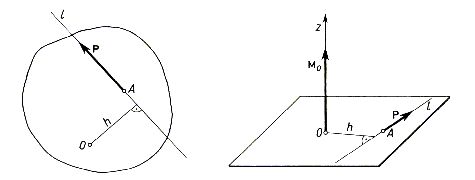
Rys. 2.7                                   Rys.2.8

Wprowadzimy teraz pewne nowe pojęcie związane z pojęciem siły, a mianowicie pojęcie momentu siły względem punktu. Otóż momentem siły względem punktu O nazywa się wektor, którego wartość bezwzględna równa jest iloczynowi wartości liczbowej siły P i ramienia tej siły względem punktu O. Wektor ten, który oznaczymy przez M0, poprowadzimy z punktu O prostopadle do płaszczyzny przesuniętej przez linię działania siły oraz przez punkt O i skierujemy w ten sposób, aby dla obserwatora patrzącego z jego końca na tę płaszczyznę, kierunek obrotu, który siła P stara się wywołać względem punktu O, był przeciwny do kierunku ruchu wskazówek zegara (rys. 2.8).
Zgodnie z wyżej podanym określeniem, moment siły nie zależy od punktu przyłożenia siły na jej linii działania, a wartość bezwzględną momentu określa wzór (2.9), z którego wynika, że moment siły jest równy zeru wtedy, gdy P=0 lub h=0, tzn. gdy siła jest równa zeru lub gdy jej linia działania przechodzi przez punkt O, względem którego wyznaczamy moment.

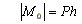(2.9)

Twierdzenie Varignona. Moment względem dowolnego punktu O wypadkowej dwu sil równy jest sumie momentów tych sil względem tegoż punktu O.
Powyższe twierdzenie możemy uogólnić dla dowolnego płaskiego układu sił zbieżnych P₁, P₂, ..., P_n. Stosując je bowiem najpierw do wypadkowej sił P₁ i P₂, następnie do wypadkowej siły P₃ oraz poprzednio znalezionej wypadkowej itd., znajdziemy, że moment względem dowolnego punktu O wypadkowej całego układu równy jest sumie momentów sił P₁, P₂, ..., P_n, czyli

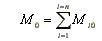(2.10)

Na podstawie twierdzenia Varignona możemy wyznaczyć moment siły P, gdy znane są współrzędne jej punktu przyłożenia w prostokątnym układzie Oxy oraz składowe P_x i P_y tej siły. Na rysunku 2.9 przedstawiona jest siła P przyłożona do punktu A o współrzędnych x, y. Obliczymy moment tej siły względem początku układu, tj. punktu O.

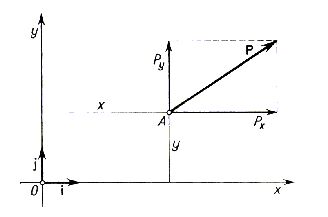
Rys. 2.9

Siłę P możemy traktować jako wypadkową dwu sił i P_x oraz j P_y równoległych do osi układu współrzędnych. Zgodnie z równaniem (2.5) mamy więc

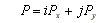(2.11)

Obliczając moment siły P jako równy sumie momentów sił i P_x oraz j P_y, których ramiona względem punktu O są równe odpowiednio y i x, otrzymujemy

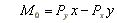(2.12)

Siła i P_x stara się wywołać obrót względem punktu O w kierunku zgodnym z kierunkiem ruchu wskazówek zegara i stąd pochodzi znak minus przed iloczynem P_xy.
Jak zostało stwierdzono wyżej, ze moment siły względem punktu jest równy zeru w dwóch przypadkach; gdy siła jest równa zeru lub gdy jej linia działania przechodzi przez dany punkt. Z własności tej można skorzystać przy rozwiązaniu zagadnień dotyczących równowagi płaskich układów sił zbieżnych.
Rysunek 2.10 przedstawia układ sił przyłożonych do punktu A pewnego ciała. Jeżeli suma momentów tych sil względem jakiegoś punktu B jest równa zeru, to na podstawie (2.13) możemy wnioskować, że albo ich wypadkowa R jest równa zeru albo linia działania tej wypadkowej przechodzi przez punkt B. Gdy okaże się jeszcze, że suma momentów sił układu względem innego dowolnego punktu C nie leżącego na jednej prostej z punktami A i B jest także równa zeru, wówczas możemy twierdzić, że wypadkowa R musi być równa zeru. W przeciwnym bowiem przypadku jej linia działania musiałaby przechodzić przez punkty A, B i C, co jest niemożliwe. Na podstawie powyższego możemy sformułować następujący warunek równowagi płaskiego układu sił zbieżnych:
Aby płaski układ sił zbieżnych znajdował się w równowadze, muszą równać się zeru sumy momentów wszystkich sił tego układu względem dowolnych dwóch punktów nie leżących z punktem przyłożenia sił na jednej linii prostej. Wynikają stąd następujące dwa równania równowagi wyrażone przez momenty:

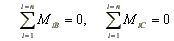(2.13)


Rys. 2.10