1.1. Podstawowe pojęcia statyki
1.1.1. Rodzaje sił
Rysunek 1.1 przedstawia ciało o ciężarze G, podparte w trzech miejscach A, B, C i obciążone siłami F1, F2, F3, F4. W miejscach podparcia wystąpią też pewne siły R1, R2, R3 (gdyż w miejscach tych następuje bezpośrednie działanie ciał na siebie). Wszystkie siły zaznaczone na rysunku, a więc F1, F2, F3, F4, G, R1, R2, R3 są działaniami pochodzącymi od innych ciał znajdujących się na zewnątrz danej bryły. Nazywamy je siłami zewnętrznymi. Siły zewnętrzne dzieli się na czynne, które dążą do wywołania ruchu lub do jego zmiany (siły F1, F2, F3, F4, G), oraz siły bierne, które przeciwdziałają ruchowi i występują w miejscach podparcia (siły R1, R2, R3 na rys. 1.1). Siły bierne nazywamy również reakcjami. Siły te pojawiają się w miejscach podparcia w chwili przyłożenia sił czynnych i znikają w chwili odciążenia ciała z tych sił czynnych.
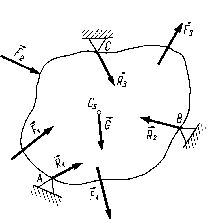
Rys. 1.1
Wewnątrz każdego ciała działają również pewne siły. Są to siły wewnętrzne, które dzielimy na siły międzycząsteczkowe i naprężenia. Pierwsze z nich są siłami działającymi pomiędzy poszczególnymi cząsteczkami materii. Naprężenia są to siły powstałe wewnątrz ciała na skutek działania nań sił zewnętrznych. Naprężenia występują w ciele zawsze parami i wzajemnie się równoważą.
Omówiony podział sił przedstawiono schematycznie na rys. 1.2.
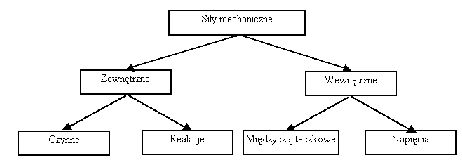
Rys. 1.2
1.1.2. Układy sił i ich podział
Zbiór dowolnej liczby sił jednocześnie działających na ciało nazywamy układem sił. W zależności od położenia linii działania sił układy możemy podzielić na dwa rodzaje:
Układ płaski odznacza się tym, że wszystkie siły tworzące ten układ leżą w jednej płaszczyźnie. Układy te można podzielić na:
Układem płaskim zbieżnym nazywa się zbiór sił, których linie działania przecinają się w jednym punkcie. Na rys. 1.3 jest przedstawiony ciężar wiszący na dwu linach. Jest to układ trzech sił zbieżnych, ciężar oraz dwie siły oddziaływania lin i Fs1, Fs2 których linie działania przecinają się w punkcie O.
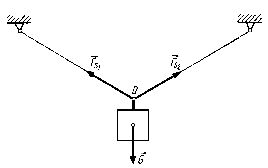
Rys. 1.3
Płaskim układem równoległym nazywa się zbiór sił, których linie działania są do siebie równoległe. Szczególnym przypadkiem takiego układu są siły działające wzdłuż wspólnej prostej. Na rys. 1.4 przedstawiono poziomą belkę obciążoną układem równoległym złożonym z pięciu sił (trzy siły czynne i dwie reakcje). Jest to przykład układu sił równoległych.
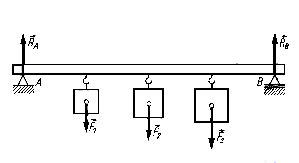
Rys. 1.4
Układ płaski dowolny jest zbiorem sił o różnych kierunkach działania. Na rys. 1.5 przedstawiony jest wiązar dachowy obciążony dowolnym płaskim układem sił. Są tutaj trzy siły czynne oraz dwie siły reakcji.
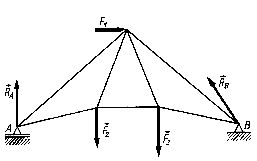
Rys. 1.5
1.1.3. Pojęcie więzów
Czynniki ograniczające swobodę ciała nazywamy więzami. Dla obracającego się w skrzyni biegów wału maszynowego więzami są jego łożyska. Dla przesuwającego się suportu tokarki więzami jest stół z prowadnicami. Dla wiszącego na linie ciężaru więzem jest sama lina. Dla pociągu więzami są tory, a dla leżącego na stole ciała więzem jest ten stół.
Ciało swobodne (bez więzów) ma sześć stopni swobody. Można to sobie interpretować następująco. W przestrzennym układzie współrzędnych (x, y, z) ciało swobodne może przesuwać się wzdłuż osi x, y, z (trzy ruchy składowe) oraz może obracać się dookoła tych trzech osi (też trzy ruchy składowe). Tak więc ciało swobodne ma 6 stopni swobody, gdyż w przestrzeni może wykonywać 6 ruchów składowych (trzy przesunięcia i trzy ruchy obrotowe). Wprowadzając więzy odbieramy ciału pewne liczbę stopni swobody. Tak np. poruszający się tłok ma jeden stopień swobody (może poruszać się wzdłuż jednej osi). Również jeden stopień swobody mają wszystkie ciała obracające się dookoła stałej osi (wałki, koła zamachowe, koła zębate, tarcze szlifierskie itp.). Przesuwana po stole płytka ma trzy stopnie swobody, bo może wykonywać trzy ruchy składowe: przesunięcia wzdłuż osi x i y oraz ruch obrotowy dookoła osi z, prostopadłej do płaszczyzny stołu.
Każde ciało działa na więzy ograniczające jego swobodę pewnymi siłami. Tak np. książka leżąca na poziomym stole naciska na stół siłą równą ciężarowi książki, wiszący na nici kamień napina tę nić siłą równą ciężarowi tego kamienia. Podobnie pociąg naciska na szyny, a obracający się wałek naciska pewnymi siłami na łożysko. Zgodnie z zasadą działania i przeciwdziałania (znana z fizyki zasada dynamiki) więzy oddziaływają na ciało z siłą równą naciskowi na więzy, lecz zwróconą przeciwnie.
1.1.4. Siły reakcji
Wprowadzenie więzów jest równoznaczne z działaniem na ciało sił biernych, czyli reakcji (siły, jakimi więzy oddziałują na ciało nieswobodne). Najczęstszymi sposobami podparcia ciał sztywnych są: przegub walcowy, przegub kulisty, podpora przegubowa stała, zawieszenie na cięgnach wiotkich, oparcie o gładką powierzchnię, oparcie o chropowatą powierzchnię, utwierdzenie całkowite, podparcie na prętach zamocowanych przegubowo na obu końcach.
Przegub walcowy.
Ciało sztywne jest osadzone na walcowym sworzniu przechodzącym przez kołowy otwór wykonany w tym ciele. Po ominięciu siły tarcia linia działania siły reakcji będzie przechodziła przez oś sworznia. Występujące dwie składowe Rx i Ry stanowią dwie niewiadome i umożliwiają wyznaczenie wartości reakcji R i jej kierunku (Rys. 1.6).
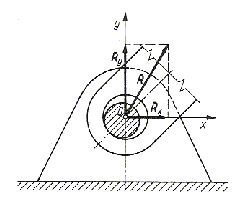
Rys. 1.6
W celu unieruchomienia punktu podparcia w przestrzeni stosuje się przeguby kuliste, które krępują swobodę przesunięć, ale umożliwiają obrót wokół dowolnej osi. Ich zakończenie jest wykonane w kształcie kuli, która jest osadzona w łożysku kulistym. Po pominięciu sił tarcia w przegubie kulistym pozostaje reakcja R o dowolnym kierunku w przestrzeni, przechodząca przez środek kuli i mająca trzy niezależne składowe Rx, Ry i Rz (rys. 1.7).
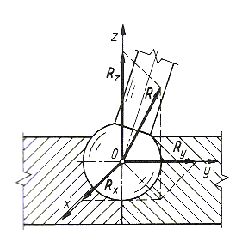
Rys. 1.7
Ponieważ opór przy przesuwaniu takiej podpory w kierunku poziomym jest bardzo mały, przyjmuje się, że linia działania reakcji jest prostopadła do płaszczyzny poziomej (przesuwu) (rys. 1.8).
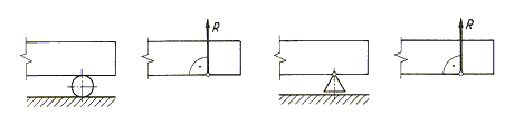
Rys. 1.8
W przypadku zastosowania podpory przegubowej stałej koniec podparcia ciała sztywnego może się obracać dookoła osi przegubu, ale nie może się przemieszczać w dwóch kierunkach. Przy założeniu, że w przegubie nie ma tarcia, linia działania reakcji R przechodzi przez punkt A. Powstają dwie niezależne od siebie składowe reakcje Rx iRy. Rozważając podporę przegubową stałą w przestrzeni należy zauważyć, że koniec podparcia B nie może się przemieszczać w trzech kierunkach i dlatego występują trzy niezależne składowe reakcje Rx, Ry i Rz (rys. 1.9).

Rys. 1.9
Podwieszenie ciała za pomocą wiotkich cięgien stwarza tzw. podpory kierunkowe jednostronne, bo cięgna mogą być tylko rozciągane. Reakcje S1 i S2 działają na ciało wzdłuż tych cięgien, zgodnie z rysunkiem (rys. 1.10).
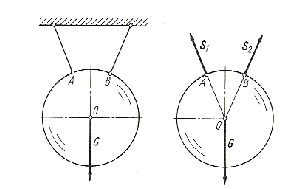
Rys. 1.10
W przypadku oparcia ciała o gładką powierzchnię (styk punktowy) występuje jedna reakcja RA, prostopadła do powierzchni styku. Jeżeli powierzchnia będzie chropowata, to wystąpią dwie składowe reakcji RA: normalna do powierzchni N i styczna siła tarcia T (rys. 1.11).
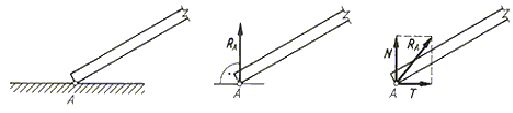
Rys. 1.11
Gdy chodzi o zupełne unieruchomienie ciała, wtedy stosuje się utwierdzenie całkowite. Ciało sztywne na płaszczyźnie ma trzy stopnie swobody, a więc wystąpi reakcja R o dwóch składowych Rx i Ry oraz moment utwierdzenia M. Rozważając całkowite unieruchomienie ciała w przestrzeni, należy zastosować takie utwierdzenie, które przedstawia sześć więzów. Wystąpi wtedy reakcja R o trzech składowych Rx, Ry i Rz oraz moment utwierdzenia M o trzech składowych Mx, My i Mz (rys. 1.12).
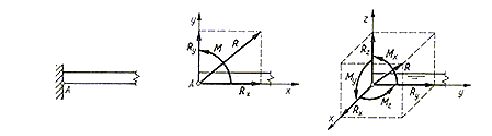
Rys. 1.12
Ciało sztywne można także unieruchomić przez podparcie na prętach zakończonych przegubami. Jeżeli pominiemy ciężary własne prętów i tarcie w przegubach, to reakcje na ciało będą działać wzdłuż tych prętów SA, SB i SC, zgodnie z rysunkiem 1.13.
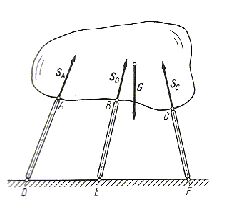
Rys. 1.13